Atividade 4

Criar função flor3(x, y, r) que cria uma flor como a figura abaixo. Depois chamá-la 100 vezes com posições e raios randômicos. Mostrar o código e discutir a regra de criação'

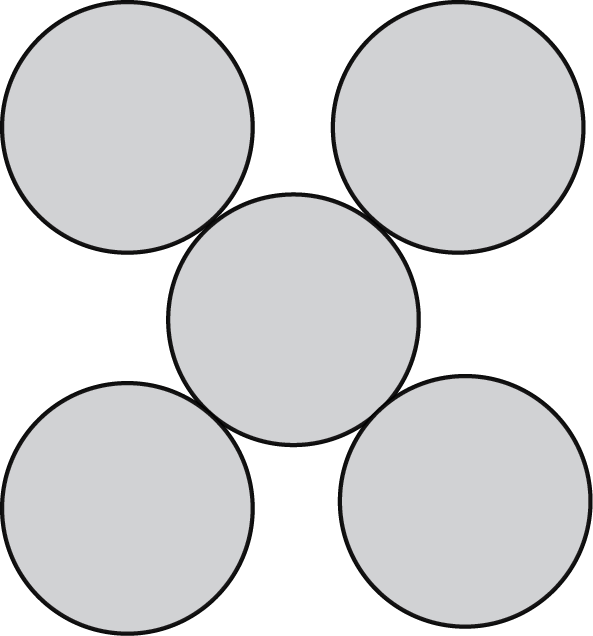
Primeiro, se faz necessário construir a função adequada para o desenho da flor requerida.Para tanto, precisamos da distância entre o centro do círculo central e suas 'pétalas' circunvizinhas.

Sabendo que seus centros estão alinhados, podemos esboçar o esquema abaixo:

A hipotenusa do triângulo do esquema é igual a 2R. Chamando os lados do triângulo isósceles de Lt, teremos, a partir do teorema de Pitágoras que:

○ 2(Lt)²=2R²

○ Lt=2R/√¯2

Logo podemos iniciar o código:

int cont=0; void setup(){ size(1000,1000); }

void circulo(float x,float y,float r){

ellipse(x,y,r*2,r*2); }

void flor2(float x, float y,float r){

float Lt=2*r/sqrt(2); circulo (x,y,r); fill(int(random(0,255)),int(random(0,255)),int(random(0,255))); circulo (x-Lt,y+Lt,r); circulo (x+Lt,y+Lt,r); circulo (x+Lt,y-Lt,r); circulo (x-Lt,y-Lt,r); fill(int(random(0,255)),int(random(0,255)),int(random(0,255)));

}

void draw(){ while(cont<100){

flor2( random(10,999),random(10,999),random(5,30));

cont++;

}

}

Note que,para gerar os valores aleatórios exigidos pelo problema, utilizei a função random.Como os parâmetros da função fill são do tipo(int,int,int) fez-se necessário utilizar a conversão.

Eis o resultado final:

#AtividadesMAM